Multibody Dynamics B

TUDelft course on multibody dynamics, ME41055

Course Description
In this course we will cover a systematic approach to the generation and solution of equations of motion for mechanical systems consisting of multiple interconnected rigid bodies, the so-called multibody systems. This course differs from “advanced dynamics”, which mostly covers theoretical results about classes of idealized systems (e.g. Hamiltonian systems), in that the goal here is to find the motions of relatively realistic models of systems (including, for example, motors, dissipation and contact constraints). By the end of the course you will be competent at finding the motions of linked rigid body systems in two and three dimensions including systems with various kinematic constraints (sliding, hinges and rolling, closed kinematic chains). Collisional interactions will be considered in a unified manner for all the dfferent ways of formulating the equations of motion. There will be weekly homework assignments and a digital exam. The homework is usually due a week after hand-out and will be graded. The homework is strictly individual but in doing the homework I encourage you to work together and to use computer software like Matlab, Maple, Adams, Working Model etc.

Course topics

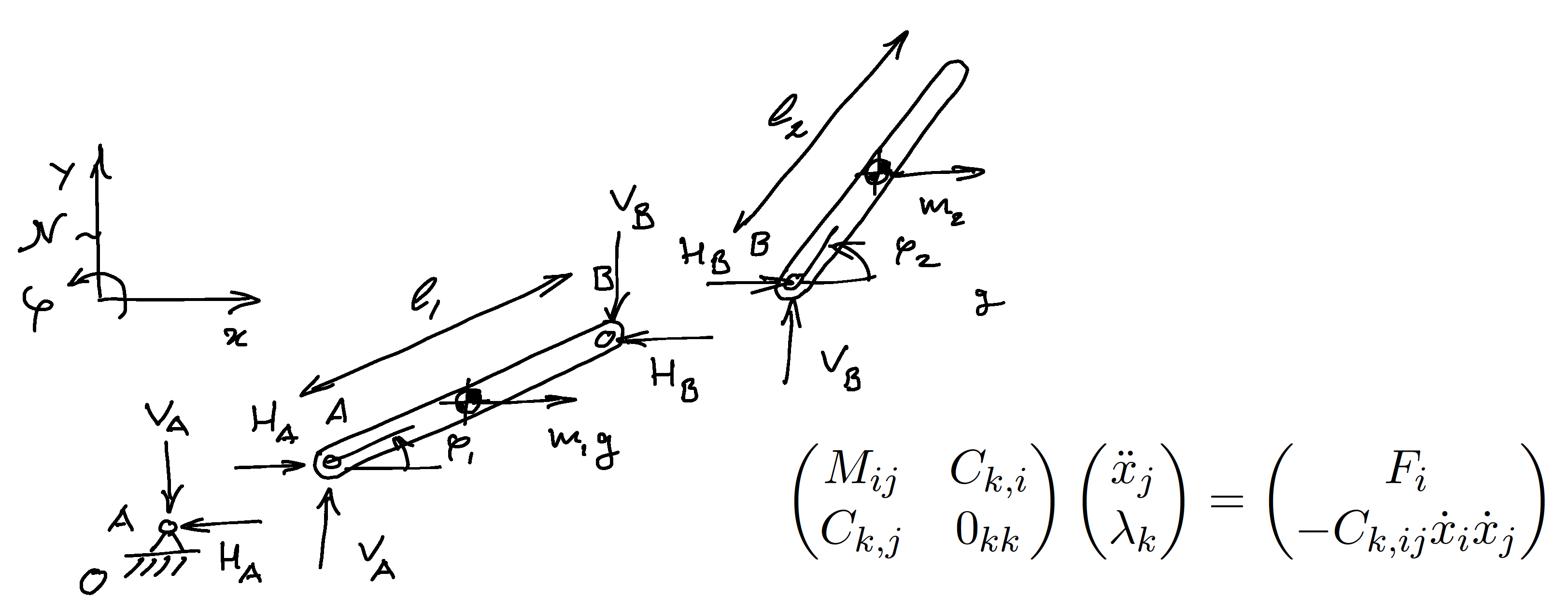
  • Newton-Euler equations of motion for a simple planar system, free body diagrams, constraint equations and constraint forces, uniqueness of the solution.
  • Systematic approach for a system of interconnected rigid bodies, virtual power method and Lagrangian multipliers.
  • Transformation of the equations of motion in terms of generalized independent coordinates, and Lagrange equations.
  • Non-holonomic constraints as in rolling without slipping, degrees of freedom and kinematic coordinates.
  • Unilateral constraints as in contact problems.
  • Numerical integration of the equations of motion, stability and accuracy of the applied methods.
  • Numerical integration of a coupled differential and algebraic system of equations (DAE’s), Baumgarte stabilisation, projection method and independent coordinates.
  • Newton-Euler equations of motion for a rigid three-dimensional body, the need to describe orientation in space, Euler angles, Cardan angles, Euler parameters and Quaternions.

Course textbook: Advanced Dynamics Heike Vallery and Arend L. Schwab Stichting Newton-Euler, Delft, The Netherlands, 3rd ed., August 2022, 636 pages ISBN: 978-90-8309-060-3 Free download

Lectures: For the second part of the book, on Multibody Dynamics, there are series of lectures available at my youtube channel. These lectures were recorded at TUDelft for the MSc level course on Multibody Dynamics B, ME41055:

Questions, comments, or suggestions? Send us an email. arendschwab@gmail.com